Seção 4.3 Teorema de Rolle e do Valor Médio
Subseção 4.3.1 Teorema do Valor Médio
Teorema 4.3.1.
(Teorema de Weierstrass)
Seja \(f\) uma função contínua no intervalo \([a, b]\text{,}\) então existem \(x_1\) e \(x_2\) em \([a, b]\) tais que
Demonstração.
Veja págino 81 do livro [5.2].
Exemplo 4.3.2.
Seja \(f=(x^3-10x^2+50)/15\text{.}\)
Teorema 4.3.4.
(Teorema de Rolle)
Seja \(f\) uma função contínua no intervalo \([a, b]\text{,}\) derivável em \((a, b)\) com \(f(a)=f(b)\text{,}\) então existirá pelo menos um \(c\in (a, b)\) tal que \(f'(c)=0\text{.}\)
Demonstração.
Caso 1: \(f\) é constante em \([a, b]\text{.}\) Neste caso \(f'(x)=0\) em \((a, b)\text{,}\) logo, para qualquer \(c\in (a, b)\text{,}\) temos \(f'(c)=0\text{.}\)
Caso 2: \(f\) não é constante em \([a, b]\text{.}\) Como \(f\) é contínua em \([a, b]\text{,}\) pelo Teorema de Weierstrass (Teorema 4.3.1), existem \(x_1\) e \(x_2\) em \([a, b]\text{,}\) tais que \(f(x_1)\) e \(f(x_2)\) são, respectivamente, os valores mínimo e máximo de \(f\) em \([a, b]\text{.}\) Como \(f\) não é constante, temos \(f(x_1)\neq f(x_2)\) e como \(f(a) = f(b)\text{,}\) necessariamente \(x_1\) ou \(x_2\) pertence a \((a, b)\text{.}\) Daí, como a derivada nos pontos de mínimo e máximo são iguais a zero, temos \(f'(x_1)=0\) ou \(f'(x_2)=0\text{.}\) Portanto, existe \(c\) em \((a, b)\) tal que \(f'(c)=0\text{.}\)
Teorema 4.3.6.
Teorema do Valor Médio (TVM).
Se \(f\) for contínua no intervalo \([a, b]\) e derivável em \((a, b)\text{,}\) então existirá pelo menos um \(c\) em \((a, b)\) tal que
Demonstração.
Considere a função \(g(x)\text{,}\) com \(x\in[a, b]\text{,}\) dada por
Observe que \(g(a)=g(b)\) e que
Pelo Teorema de Rolle (Teorema 4.3.4), existe \(c\in(a, b)\) tal que
Ou seja,
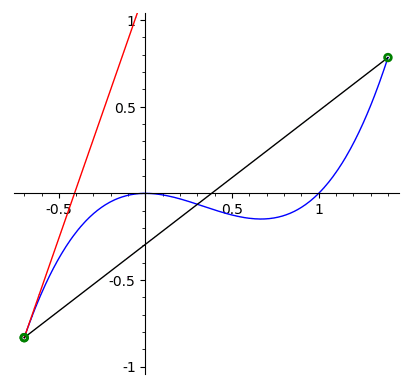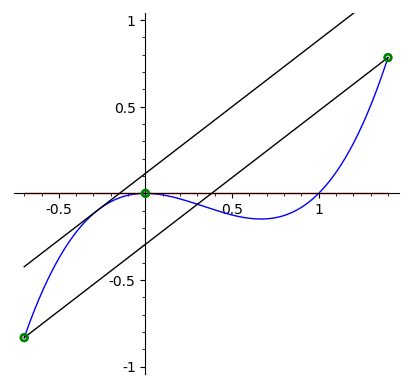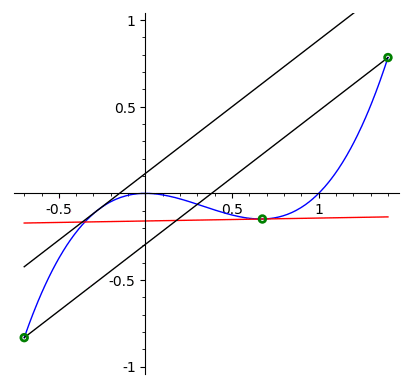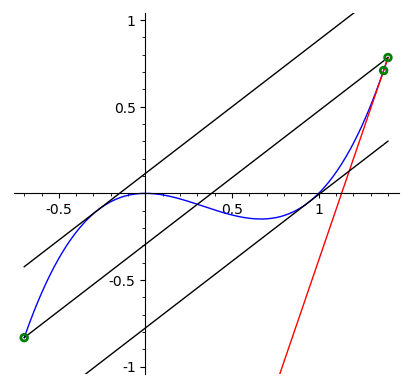
Exemplo 4.3.7.
Seja \(f=x^3-x^2\text{.}\) No intervalo \([-7/10, 14/10]\text{,}\) existem dois pontos \(c_1\) e \(c_2\text{,}\) nos quais,
Subseção 4.3.2 Aplicações do Teorema do Valor Médio
Como consequência do Teorema do Valor Médio (TVM), temos o seguinte teorema:
Teorema 4.3.9.
Seja \(f\) contínua no intervalo \((a,b)\text{.}\)
- Se \(f'(x)>0\) para todo \(x \in (a,b)\text{,}\) então \(f\) será estritamente crescente em \((a,b)\text{.}\)
- Se \(f'(x)\lt 0 \) para todo \(x \in (a,b)\text{,}\) então \(f\) será estritamente decrescente em \((a,b)\text{.}\)
Demonstração.
item a) Já que \(f'(x)>0\text{,}\) \(\forall x \in (a, b)\text{,}\) sejam, \(c, d \in (a, b)\text{,}\) com \(c\lt d\text{.}\) Vamos mostrar que \(f(c)\lt f(d).\) Como \(f\) satisfaz as hipóteses do TVM, existe \(\tilde{x}\in (c, d)\) tal que
Como \(f'(\tilde{x})>0\text{,}\) pois \(\tilde{x}\in (a,b)\) e \(d-c>0,\) segue
Portando, como a escolha de \(c \lt d\text{,}\) foi arbitrária, o resultado segue.
item b) Este item é análogo ao anterior.
Exemplo 4.3.10.
Determine os intervalos de crescimento e de decrescimento de \(f(x) = x^3-5x^2+3x+1\text{.}\)
Soluçãoe
Como o gráfico de \(f'(x)\) é uma parábola, sabemos que
Como \(f\) é contínua, pelo Teorema 4.3.9, temos
Exemplo 4.3.11.
Determine os intervalos de crescimento e de decrescimento de
Definição 4.3.12.
Sejam \(f\) uma função derivável no intervalo \((a,b)\) e \(T_p(x)\) a reta tangente em \((p, f(p))\) ao gráfico de \(f\text{,}\) \(p\in (a, b)\text{.}\)
Dizemos que \(f\) tem concavidade para cima em \((a, b)\) se
\begin{equation*} f(x)>T_p(x) \end{equation*}para quaisquer \(x\) e \(p\) em \((a, b)\text{,}\) com \(x\neq p\text{.}\)
Dizemos que \(f\) tem concavidade para baixo em \((a, b)\) se
\begin{equation*} f(x)\lt T_p(x) \end{equation*}para quaisquer \(x\) e \(p\) em \((a, b)\text{,}\) com \(x\neq p.\)
Definição 4.3.13.
Sejam \(f\) uma função e \(p\in D_f\text{,}\) com \(f\) contínua em \(p\text{.}\) Dizemos que \(p\) é ponto de inflexão de \(f\) se existem \(a, b \in D_f\text{,}\) com \(p\in (a, b)\text{,}\) tal que as concavidades de \(f\) em \((a, p)\) e em \((p, b)\) sejam opostas.
Teorema 4.3.14.
Seja \(f\) uma função que admite derivada até 2ª ordem no intervalo \((a, b)\text{.}\)
- Se \(f''(x)>0\) para \(x \in (a,b)\text{,}\) então \(f\) terá concavidade para cima em \((a, b)\text{.}\)
- Se \(f''(x)\lt 0\) para \(x \in (a,b)\text{,}\) então \(f\) terá concavidade para baixo em \((a, b)\text{.}\)
Demonstração.
item a) Sejam \(f''(x)>0\) para \(x \in (a,b)\) e \(p \in (a, b)\) arbitrário. Vamos mostrar que
para todo \(x\in (a, b)\text{,}\) com \(x\neq p\text{,}\) na qual, \(T_p(x) = f'(p)(x-p)+f(p)\text{.}\) Considere \(g(x) = f(x)-T_p(x)\text{,}\) logo
pois \(T_p'(x) = f'(p)\text{.}\) Como \(f''(x)>0\) em \((a, b)\text{,}\) pelo Teorema 4.3.9, \(f'\) é estritamente crescente em \((a, b)\text{.}\) Então,
Mais uma vez pelo Teorema 4.3.9,
Como \(g(p)=0\text{,}\) temos \(g(x)>0\) para todo \(x\in(a, b)\text{,}\) \(x\neq p\text{.}\) E como \(g(x) = f(x) - T_p(x)\text{,}\) temos
Exemplo 4.3.15.
Estude a função
com relação à concavidade e pontos de inflexão.
SoluçãoExemplo 4.3.16.
Estude a função
com relação à concavidade e pontos de inflexão.
DicaExercícios 4.3.3 Exercícios
1.
Determine os intervalos de crescimento e de decrescimento das funções e esboce o gráfico das funções:
- \(\displaystyle f(x) = x^3-3x^2+1\)
- \(\displaystyle f(x) = x^3+2x^2+x+1\)
- \(\displaystyle f(x) = x+\frac{1}{x}\)
- \(\displaystyle f(x) = 3x^5-5x^3\)
- \(\displaystyle f(x) = e^{2x}-e^x\)
- \(\displaystyle f(x) = \frac{x^3-x^2+1}{x}\)
- \(\displaystyle f(x) = xe^x\)
- \(\displaystyle f(x) = \frac{\ln{x}}{x}\)
- \(\displaystyle f(x) = \frac{x^2-x+1}{2x-2}\)
- \(\displaystyle f(x) = x-e^x\)
2.
Estude a função dada com relação à concavidade e pontos de inflexão.
- \(\displaystyle f(x) = x^3-3x^2+1\)
- \(\displaystyle f(x) = x^3+2x^2+x+1\)
- \(\displaystyle f(x) = x+\frac{1}{x}\)
- \(\displaystyle f(x) = 3x^5-5x^3\)
- \(\displaystyle f(x) = e^{2x}-e^x\)
- \(\displaystyle f(x) = \frac{x^3-x^2+1}{x}\)
- \(\displaystyle f(x) = xe^x\)
- \(\displaystyle f(x) = \frac{\ln{x}}{x}\)
- \(\displaystyle f(x) = \frac{x^2-x+1}{2x-2}\)
- \(\displaystyle f(x) = x-e^x\)