Seção 3.1 Derivadas: Conceito e Interpretação Geométrica
O conceito de derivada está relacionado ao conceito de reta tangente ao gráfico de uma função \(f:A\subset\mathbb{R}\rightarrow B\subset\mathbb{R}\text{.}\)
Antes de definir a reta tangente ao gráfico de uma função \(f(x)\) no ponto \((p, f(p))\text{,}\) vamos escrever a equação da reta \(r_x\text{,}\) que passa pelos pontos \((p, f(p))\) e \((x, f(x))\text{.}\)
Definição 3.1.2.
Chama-se coeficiente angular de uma reta \(r\) de inclinação \(\alpha,~\alpha\neq \pi/2\text{,}\) o número \(m\) tal que \(m = \tan{\alpha}\text{.}\)
Teorema 3.1.3.
Se \(r\) é uma reta não-vertical que passa pelo ponto \((x_0, y_0)\) e tem coeficiente angular \(m\text{,}\) então uma equação de \(r\) é
Tal equação é denominada equação fundamental da reta.
Observação 3.1.4.
O coeficiente angular da reta \(r_x\text{,}\) que passa pelos pontos \((p, f(p))\) e \((x, f(x))\) é dado por:
E a equação da reta que passa por \((p, f(p))\) e \((x, f(x))\) é dada por
Definição 3.1.6.
A reta \(T_p\) tangente ao gráfico de \(f\) é obtida fazendo \(x\) tender a \(p\text{,}\) na equação da reta \(r_{x}\text{:}\)
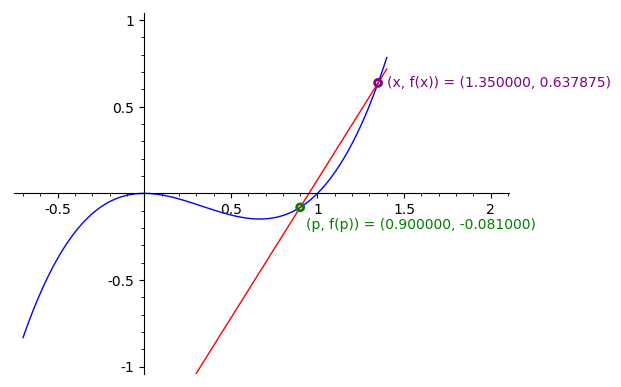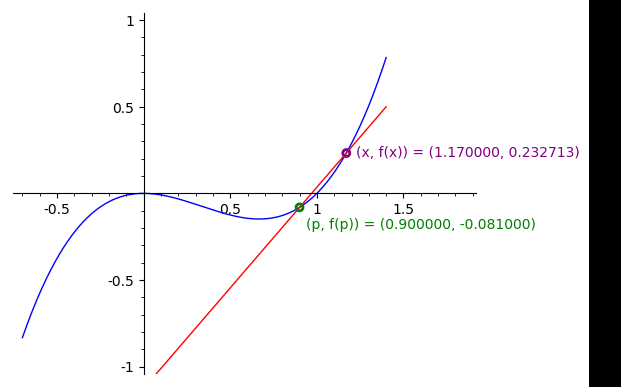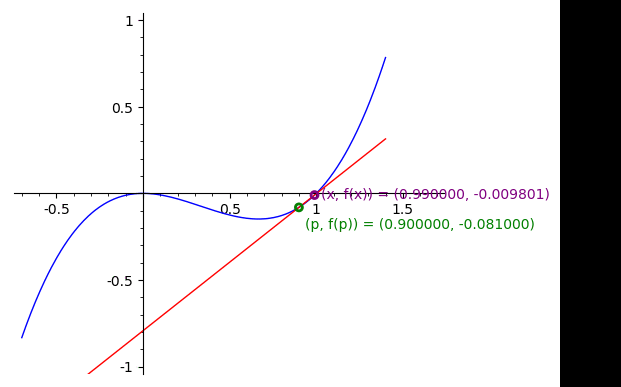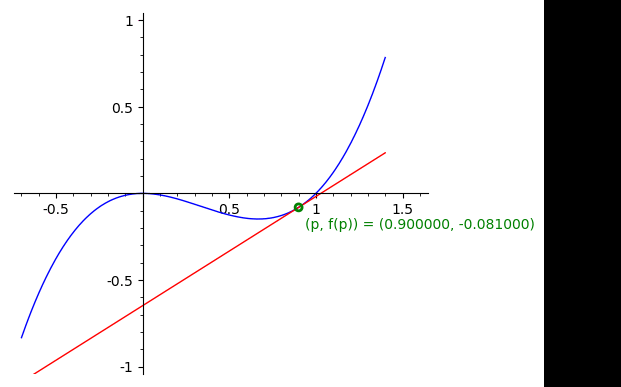
Definição 3.1.8.
Sejam \(f:A\rightarrow B\) uma função e \(p\) um ponto do domínio de \(f\text{.}\) O limite
quando existe e é finito, denomina-se derivada de \(f\) em \(p\) e é indicada por \(f'(p)\text{.}\) Assim,
Se \(f\) admite derivada em \(p\text{,}\) então diremos que \(f\) é diferenciável em \(p\text{.}\) A função \(f\) é diferenciável em um intervalo aberto \((p,q)\) (ou \((p, \infty)\) ou \((-\infty, p)\) ou \((-\infty, \infty)\)) se for diferenciável em cada ponto do intervalo.
Observação 3.1.9.
Segue da definição de limites que
- \(\displaystyle f'(p) = \lim_{x\rightarrow p} \frac{f(x)-f(p)}{x-p};\)
- \(\displaystyle f'(p) = \lim_{h\rightarrow 0} \frac{f(p+h)-f(p)}{h};\)
- A reta tangente ao gráfico de \(f\text{,}\) no ponto \((p, f(p))\text{,}\) é dada por\begin{equation*} y-f(p) = f'(p)(x-p). \end{equation*}
Exemplo 3.1.10.
Seja \(f(x)=x^2\text{.}\)
- Calcule a derivada de \(f\) no ponto \(x=1.\)
- Encontre a equação da reta tangente ao gráfico de \(f\) no ponto \((1,f(1))\text{.}\)
Exemplo 3.1.11.
Mostre que \(f(x)=|x|\) não é derivável em \(p=0\text{.}\)
DicaCalcule
- \(\displaystyle \lim_{x\rightarrow 0^+} \frac{f(x)-f(0)}{x-0}\)
- \(\displaystyle \lim_{x\rightarrow 0^-} \frac{f(x)-f(0)}{x-0}\)
Subseção 3.1.1 A Derivada como uma Função
Exemplo 3.1.12.
Seja \(f(x)=x\text{,}\) calcule \(f'(x)\text{.}\)
SoluçãoExemplo 3.1.13.
Seja \(f(x)=x^2\text{,}\) calcule \(f'(x)\text{.}\)
SoluçãoExemplo 3.1.14.
Seja \(f(x)=x^3-x^2\text{,}\) encontre uma fórmula para \(f'(x)\text{.}\)
Exercícios 3.1.2 Exercícios
1.
Calcule \(f'(x)\) pela definição (através do limite), nos seguintes casos;
- \(\displaystyle f(x)=x^{2}+x\)
- \(\displaystyle f(x)=x^{3}\)
- \(\displaystyle f(x)=5x\)
- \(\displaystyle f(x)=3x-1\)
- \(\displaystyle f(x)=\frac{1}{x}\)
- \(\displaystyle f(x)=\frac{1}{x^{2}}\)
2.
Para cada item da questão 1, determine a equação da reta tangente ao gráfico de \(f\) no ponto \((1, f(1))\text{.}\)